A hatványozás

Ha sok ugyanolyan számot kell összeadni, akkor megkönnyíthetjük a dolgunkat úgy, hogy szorzást végzünk.
Például ha van 3 perselyünk, és mindegyikben négy darab húszforintos van, akkor legkönnyebben úgy számolhatjuk ki,
hogy hány húszforintossal rendelkezünk, ha a 3-at megszorozzuk 4-gyel.
Azért ennyivel, mert 3 perselyünk van, és mindegyikben 4 darab húszforintos.
Tehát: 4 + 4 + 4 = 3 x 4
Például ha van 3 perselyünk, és mindegyikben négy darab húszforintos van, akkor legkönnyebben úgy számolhatjuk ki,
hogy hány húszforintossal rendelkezünk, ha a 3-at megszorozzuk 4-gyel.
Azért ennyivel, mert 3 perselyünk van, és mindegyikben 4 darab húszforintos.
Tehát: 4 + 4 + 4 = 3 x 4
Ha a 3-at megszorozzuk 4-gyel, akkor 12-t kapunk, tehát 12 húszforintos van összesen.

Ha több ugyanolyan számot szeretnénk összeszorozni, akkor van arra módunk,
hogy megkönnyítsük a műveletet. Ezt a lehetőséget hatványozásnak hívjuk.
Például ha a 3-at 4-szer kell megszorozni önmagával, akkor az így néz ki egyszerű szorzással: 3 x 3 x 3 x 3 = 81
Hatványozás során ezt sokkal rövidebben is felírhatjuk: 34 = 3 x 3 x 3 x 3 = 81
A fentiek közül a 34 a hatványalak, ami kiolvasva: három a negyediken.
Azért a negyediken, mert négyszer szoroztuk meg önmagával a 3-at.
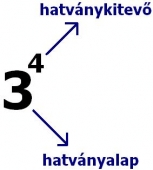
Azt a számot, amit hatványozunk, hatványalapnak hívjuk, a fölötte levő kis szám pedig a hatványkitevő.
Léteznek olyan hatványok, amelyeknek más elnevezésük is van.
Például:
52= öt a másodikon, más néven öt a négyzeten.
53= öt a harmadikon, más néven öt a köbön.
| Öt a négyzeten | Öt a köbön |
Ha jól megnéztétek, eddig csak kettő vagy annál nagyobb hatványkitevőket írtunk fel. Azonban léteznek ennél kisebbek is.
Például ha a négynek az első hatványát vesszük, akkor az így néz ki: 41.
Kiolvasva: négy az elsőn.
Ez azt jelenti, hogy a 4 csak egyszer szerepel a szorzásban, azaz ennek az eredménye 4.
A legkülönösebb hatványkitevő a nulla. Létezik olyan, hogy valamelyik számnak a nulladik hatványa.
Például 60 Kiolvasva: hat a nulladikon.
A szabály pedig a következő: bármely számnak (kivéve a nullát) a nulladik hatványa egyenlő eggyel.
Tehát 60=1
De akkor mennyi lehet a nullának a nulladik hatványa?

00= nem értelmezzük, ennek nincs eredménye!
Van még egy szabály a nullával kapcsolatban: nullának bármelyik hatványa nulla.
Például:
| 01 | = | 0 |
| 02 | = | 0 |
| 03 | = | 0 |
| 04 | = | 0 |
| 05 | = | 0 |
| stb. | ||
Ezen kívül az 1 hatványaira is vonatkozik egy szabály: egynek bármelyik hatványa egy.
Például:
| 11 | = | 1 |
| 12 | = | 1 |
| 13 | = | 1 |
| 14 | = | 1 |
| 15 | = | 1 |
| stb. | ||
Hiszen ha jobban megnézzük, akkor rájövünk,
hogy bármennyiszer is szorzom össze önmagával az egyet, az eredmény mindig egy lesz:
hogy bármennyiszer is szorzom össze önmagával az egyet, az eredmény mindig egy lesz:
1 x 1 x 1 x 1 x 1 x 1 x 1 x 1 x 1 x 1 = 1
Igényeld itt az 5 részes ingyenes feladatokat 7. osztályos gyermekednek, és meglátod, öröm lesz a tanulás!

Tanulja meg és gyakorolja játékosan a Te gyermeked is a matematikát
a Matekból Ötös oktatóprogramok segítségével!


Tovább megyek a webshopra >>>


